Understanding stack data structure

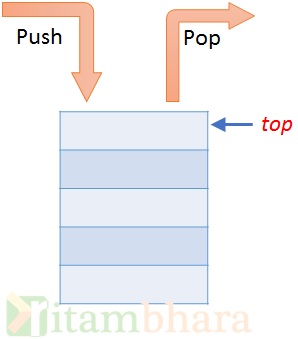Stack is a collection of objects where objects are inserted and removed in the Last-In-First-Out order. Element inserted at the end will be deleted first. It is a limited access data structure which essentially allows two operations push and pop.

Push: Inserting data at the top of stack.
Pop: deleting data from the top of stack.

The function call stack of C and C++ is a typical example of stack data structure. If we have three functions main, fun1 and fun2. main calling fun1 and fun1 calling fun2 as shown below.

int main()
{
    printf("Main - Start");
    fun1();
    printf("Main - End");
    return 0;
}
void fun1()
{
    printf("fun1 - Start");
    fun2();
    printf("fun1 - End");
}
void fun2()
{
    printf("fun2 - Start");
    printf("fun2 - End");
}

Memory Stack holding the activation record of functions called at different stages will look as below:

Output of the above code will be (with state from the above diagram mentioned along)..

    Main - Start   // State - 2
    fun1 - Start   // State - 3
    fun2 - Start   // State - 4
    fun2 - End     // State - 4
    fun1 - End     // State - 5
    Main - End     // State - 6

fun2 is the last one to be pushed in the stack but the first one to be poped out of it.
Operations

There can be many operations on stack depending on the implementation like this post, but we will discuss only three basic operations on the stack

Push – inserting element at the top of stack.
Pop – removing the top element of stack.
isEmpty – check is stack is empty or not.
print – Print the entire stack.
getTop – Returns the element at top of stack without removing it from stack.

All the operations above are constant time operations except print, which will take O(n) time where n is the number of elements in the stack.

Implementation 

Stack is essentially a linear data structure (ex. Binary Tree  is a hierarchical data structure). Because of linearity, it can either be implemented using either Array or Linked list. In both the cases, restriction will be imposed on the base data structure (array, linked list, vector, ArrayList etc) so that it is accessed using the stack operations only.

For example, If we are implementing using array, then user should not access any i’th element of array using arr[i], but should access it using pop, which will only return top element (first or last element depending on which side the stack is growing).

Hence, the underlining actual data structure will only be accessible thru stack APIs. For example, in the below Stack definition, user will not even know that the stack is implemented using Array, because the array cannot be accessed from outside

class MyStack
{
   private:
       int top;
       int arr[MAX];   // MAX - maximum number of element in stack
   public:
      // Default Constructor
      MyStack():top(-1){}
      void push(int data);   // Insert data at top position
      int pop();             // delete & return top element from array
      int getTop();          // return top element without deleting it
      int isEmpty();         // check if the array is empty or not
};

If we replace the implementation with linked list, keeping the interface same:

struct Node{
    int data;
    Node *next;
};
class MyStack
{
   private:
      Node * top;
   public:
      MyStack():top(NULL){}
      void push(int);
      int pop();
      int getTop();
      int isEmpty();
};

User will have absolutely no impact on the usage. This is also called Abstraction in Object Oriented programming.

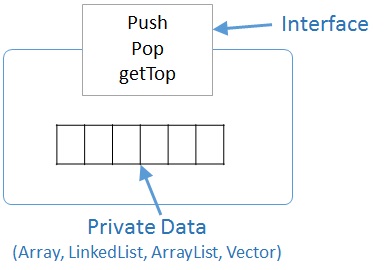
We have two separate posts discussing the Array implementation and Linked List implementation of Stack.

Applications

Stack has many applications in computer science. One of them is discussed above (function call stack).

1. Simplest application can be to reverse a word.

MyStack s;
void reverse(char *str)
{
    if(str == null)
        return;
    // Insert all the characters in the stack.
    while(*str != '\0')
        s.push(*str);
    // Pop element from Stack and add it to string from position 0.
    int i=0;
    while(!s.isEmpty())
    {
        str[i] = s.pop();
        i++;
    }
    str[i] = '\0';
}

2. Simulating recursion.

Recursive algorithms are always more time consuming than non-recursive algorithms as explained in this post. But recursive functions are sometimes very easy to write, esp. in case of Tree or Graph algorithms. ex. tree traversal algorithms. Hence, we may want to use the best of both the worlds, simulate recursion using stack.

3. Undo/Redo Mechanism

When we do undo in a text editor then the last (most recent) operation is undone. If operations are stored in a Stack then undo will be pop of the latest operation from the top of stack.

4. Polish notations and their evaluation

Stack is also used in converting from one polish notation to another, like converting from infix to postfix notation. It is also used if we write an algorithm to evaluate an expression written in postfix (or infix).

5. Backtracking algorithms

Algorithms like Sudoku or maze generation algorithms or scrabble square are implemented using stack.