Right view of a binary tree

Write code to print the right-view of a binary tree. Right-view of the tree is the nodes visible when the tree is seen from the right side. If there are two nodes at the same level, then only the right-most node will be visible in the right-view as shown below:

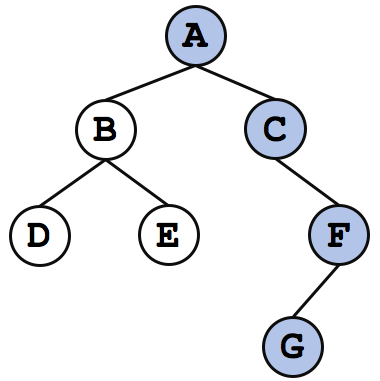
Solution:
If we traverse the binary tree in the below traversal:

1. Print the root node’s data
2. Print right sub-tree recursively
3. Print left sub-tree recursively

This is similar to pre-order traversal. The only difference is the order in which child nodes are called. The function for this traversal is

void traverseTree(Node* r)
{
    if(r == NULL) { return; } // TERMINATING CONDITION
    cout<data<<" "; traverseTree(r->right);
    traverseTree(r->left);
}

 
While traversing the tree in this traversal, we are visiting the right-most node of a particular level before visiting other nodes at that level.
The solution to this problem now is very similar to this post where we printed the left-view of tree.
Traverse the given tree in above traversal and keep a check on whether or not the right-most node at current level is printed. If no nodes for the current level is printed, print the current node, else continue traversing the tree.
We need two variables in this case,

1. A variable for the current level of node (See this post)
2. A reference variable for the maximum level upto which the left-most nodes are printed.

Below is the C++ code for this:

struct Node
{
    char data;
    Node* left;
    Node* right;
    Node(int v):data(v), left(NULL), right(NULL){}
};
void printRightView(Node *r, int level, int* maxLevel)
{
    if(r == NULL){ return; }
    if(level > *maxLevel)
    {
        printf("%c ", r->data);
        *maxLevel = level;
    }
    printRightView(r->right, level+1, maxLevel);
    printRightView(r->left, level+1, maxLevel);
}
int main(int argc, const char * argv[]) {
    Node* root = new Node('A');
    root->left = new Node('B');
    root->right = new Node('C');
    root->left->left = new Node('D');
    root->left->right = new Node('E');
    root->right->left = new Node('F');
    root->right->left->right = new Node('G');
    int maxLevel = -1;
    printRightView(root, 0, &maxLevel);
    return 0;
}