Minimum edit distance of two strings

Given two strings of size m and n respectively, find the minimum number of operations required to transform one string into another. The following thee operations are allowed

• Insert(pos, ch) – Insert a character at a position in the string.
• Delete(position) – Delete a character from a position in the string.
• Replace(position, character) – Replace a particular character with some other character at a position in the string.

For example, If input strings are ‘KITTEN‘ and ‘SITTING‘ then the edit distance between them is 3.

1. kitten -> sitten (Replace)
2. sitten -> sittin (Replace)
3. sittin -> sitting (Insert)

It can be used in applications like auto spell correction to correct a wrong spelling and replace it with the nearest (minim distance) word.

This can be more complex, and may not be intuitive. For example, the distance between two strings INTENTION and EXECUTION. then the minimum distance is 5.

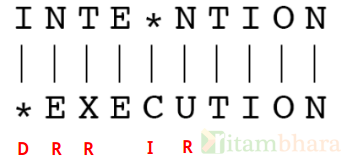
Recursive Solution:

We start from the first character and for each character, we do the following:

IF (characters of two strings are same)
    Ignore that characters and get count for remaining strings.
    (Recursively call the function for lengths m-1 and n-1).
ELSE (If last characters are not same)
    Consider all three operations on character of first string.
    Recursively compute minimum cost for all three operations and take minimum of these three values.
    1. Insert (Insert str2[j] at position i'th position in str1):
       Call function recursively for (str1, str2, i+1, j+1, m, n-1)
    2. Remove (delete char at i'th position in str1):
       Call function recursively for Recur for (str1, str2, i+1, j, m-1, n)
    3. Replace (str1[i] = str2[j]):
       Call function recursively for Recur (str1, str2, i+1, j+1, m-1, n-1)

If we traverse the array backward then we don’t need to pass variables i and j (because at any point of time we will be considering the last element in the two strings.

Also we don’t need to actually insert the characters in the string, because we are just calculating the edit distance and don’t want to alter the strings in any way.

Below is the code for the same.

Code:

/** Don't need to pass i and j if we are traversing from the last.
 */
int editDist(char* str1 , char* str2 , int m ,int n)
{
   // If any of the two strings is empty then the only option is to
   // insert all elements of other array in it.
   if (m == 0) return n;
   if (n == 0) return m;
   if (str1[m-1] == str2[n-1])
   {
      // If the two characters are same.
      return editDist(str1, str2, m-1, n-1);
   }
   else
   {
      // If two characters are not same then consider all options and return min
      // of all of them.
      return 1 + min( editDist(str1,  str2, m, n-1),    // Insert
                      editDist(str1,  str2, m-1, n),   // Remove
                      editDist(str1,  str2, m-1, n-1)); // Replace
   }
}

Clearly the solution takes exponential time.

Dynamic Programming Solution:

In the recursive solution, we are clearly solving one sub-problem multiple times. Also, the problem demonstrate the optimal sub-structure and hence seems to be a fit for dynamic programming solution.

In this approach we will solve the problem in a bottom-up fashion and store the min edit distance at all points in a two-dim array of order m*n. Let’s call this matrix, ‘Edit Distance Table‘. Initially it will be initialized as below:

editDistance[0][0] = 0;
for (int i=0; i<m; i++)
    editDistance[i][0] = i;
for (int j=0; j<n; j++)
    editDistance[0][j] = j;

Any cell (i,j) of the matrix holds the edit distance between the first (i+1) characters of str1 and (j+1) characters of str2.

We traverse the matrix and value of each cell is computed as below:

The editDistance Matrix will populate as shown below:

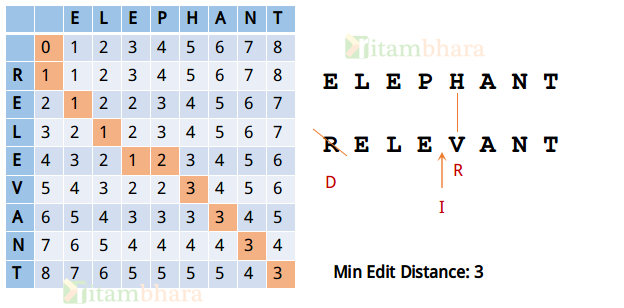
This solution takes O(n^2) time and O(n2) extra space.

Code:

int editDistDP(char* str1, char* str2, int m, int n)
{
   // Matrix to store intermediate values
   int editDistance[m+1][n+1];
   // First Column
   for (int i=0; i<m; i++)
      editDistance[i][0] = i;
   // First Row
   for (int j=0; j<n; j++)
      editDistance[0][j] = j;
   // Populate editDistance
   for(int i=1; i<=m; i++)
   {
      for (int j=1; j<=n; j++)
      {
          if(i == 0)
          {
              // First string is empty
              editDistance[i][j] = j;
          }
          else if(j == 0)
          {
              // Second String is empty
              editDistance[i][j] = i;
          }
          else if(str1[i-1] == str2[j-1])
          {
              // If both characters are same
              editDistance[i][j] = editDistance[i-1][j-1];
          }
          else
          {
              // If both characters are different.
              editDistance[i][j] = 1 + min(editDistance[i][j-1], editDistance[i-1][j], editDistance[i-1][j-1]);
        }
    }
    return editDistance[m][n];
}

Variations:

1. One variation of the question can be that Replace is treated as delete and insert and hence has a cost of 2. Now to find minimum cost we have to minimize the replace operations.
2. Given two sequences, align each others to letter or gap as shown below:

Reference:

• https://web.stanford.edu/class/cs124/lec/med.pdf
• http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Dynamic/Edit/