Maximum XOR value of two elements

Given an array of numbers find the maximum XOR value of two numbers in the array.

Input Array = {12, 15, 5, 1, 7, 9, 8, 6, 10, 13};
Output = 15 (XOR of 5 and 10)
  5 = 0101
 10 = 1010
 ---------
XOR = 1111

Solution-1. Brute Force

The brute-force solution is to consider all the pairs, compute their XOR and return the maximum of the XOR values.

This is fairly simple and straight forward O(n²) time solution.

void printMaxXOR(unsigned int * arr, int n)
{
   unsigned int maxXor = 0;
   int a = 0, b = 0;
   for(int i=0; i<n; i++)
   {
      for(int j=i+1; j<n; j++)
      {
         if(maxXor < (arr[i]^arr[j]) )
         {
            maxXor = arr[i]^arr[j];
            a = i; b = j;
         }
      }
   }
   cout<<"MAX XOR IS OF " << arr[a] << " and " << arr[b]
       << ". VALUES : " << maxXor;
}

If the function is called like:

int main()
{
   unsigned int arr[] = {12, 15, 5, 7, 1, 9, 8, 6, 10, 13};
   printMaxXOR(arr, 10);
}

Then output will be

MAX XOR IS OF 5 and 10. VALUES : 15

Solution-2: Linear Time Solution
Suppose we have a data structure, that can answer below two queries:

1. Add a number to the collection.
2. Given a number x, find the maximum XOR of x with any number in the collection.

Then for each element in the array, we will just compute the max XOR with other elements inserted till now, and then insert that element in the array. This can give us linear time solution if insertion and finding-max-XOR are constant time operations:

void printMaxXORTrie(unsigned int * arr, int n)
{
   int maxXOR = 0;
   for(int i=0; i<n; i++) { //find max XOR of a[i] with num. in collection int t = findMaxXOR( ..., a[i] ); if(t > maxXOR)
         maxXOR = t;
      // INSERT arr[i] in Collection
      insertValueInCollection( arr[i]);
   }
    cout<<"MAX XOR VALUES : "<<maxXOR;
}

The data structure we are choosing is Trie (just Binary Tree) with the following struct of Node

struct Node
{
   Node *left, *right;
   // Constructor. Set left and right to NULL
   Node():left(NULL),right(NULL){}
};

There is no data inside the Node, data is not required. Since we are dealing with Binary values (0 or 1), hence we need only two children for each node (left and right).
While inserting a number, we look into each bit of that number. If that bit is 1 then we move on right side else, if the bit is 0, we move on the left side.

We will look into both the points mentioned above. Lets look into the first part,

1. how to insert element 

Let us consider 4-bit numbers only. Let 12 (1100), 15(1111) and 5(0101) are already inserted in the Trie. Then the trie will look like:

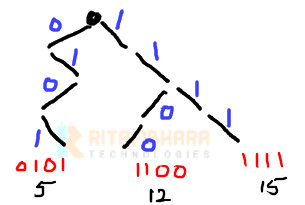
Each root-to-leaf path represent a number. When we go toward right, the edge represent 1. when we go toward left, the edge represent 0. Now, with these three numbers already in the Trie,  let us say, we want to insert 7 (0111) in it.
Now for each bit of 7 (starting from MSB) we see if the bit is already there in the Trie. If the bit is not present in the Trie, we add it.
The first two bits 01 are already present, we add the last two 11 and the Trie becomes as shown below.

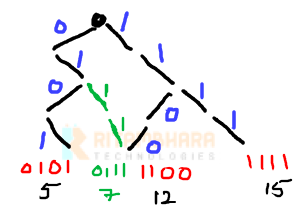
Number of leaves actually represent the count of unique numbers stored in the Trie. In above case, there are 4 numbers in the Trie (12, 15, 5 and 7).
Since number of bits in a number are constant (eg. 32). The depth of the tree is also fixed and inserting a new number will take constant time. Below is the function to insert a number in the Trie

// Create a trie from the values in the array
void insertValueInTrie(Node* r, unsigned int x)
{
   unsigned int N = sizeof(unsigned int) * 8;
   for(int i=N-1; i>=0; i--)
   {
      unsigned int bitValue = (x & (1<<i)); // Get i'th Bit of x
      if(bitValue != 0)
      {
         if(r->right == NULL)
            r->right = new Node();
         r = r->right;
      }
      else
      {
         if(r->left == NULL)
            r->left = new Node();
         r = r->left;
      }
   }
}

2. How to find the max XOR of a number with numbers stored in Trie

The second point is to find the max XOR value of a given number with all the numbers stored in the Trie.
To understand the algorithm, let us revise the flowchart of XOR

  a  b   a^b
 -- --  ----
  0  0   0
  0  1   1
  1  0   1
  1  1   0

As shown above, the result of XOR is max when the bits are not same.
If we want to compute the max XOR of x with numbers stored in Trie, then for each bit of x(starting from MSB), we try to maximise the XOR. If the bit is 1, then we need a 0 to get the max XOR. If the Trie is as shown below:

And we want to check the max XOR with x = 7 (0111). The first bit is 0, so we move toward 1, because that will give us a 1 on XOR.

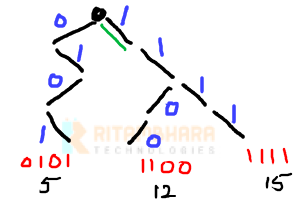
The next bit is 1, so we try toward 0. But 0 is not present (there is not number with initial two bits as 10), hence we move toward 1, and XOR at this bit is 0. The XOR till now is 10.

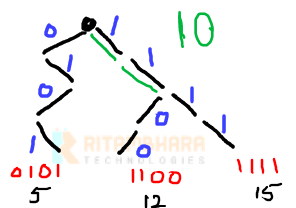
the next bit is 1, we move toward 0 making the XOR 101, similarly the last bit is 1 and we again move toward 0. The final, (maximum) XOR value is 1011.

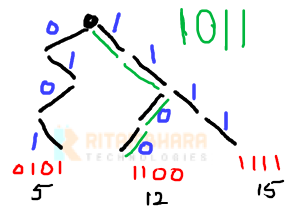
The code for this is shown below:

// Find Max XOR of x in the tree rooted at r.
unsigned int findMaxXOR(Node* r, unsigned int x, int bitPos)
{
   if(r == NULL || bitPos < 0)
      return 0;
   if(bitPos == 0)
   {
      if( (x & (1<<bitPos)) == 1)
         return (r->left == NULL) ? 0 : 1;
      else
         return (r->right == NULL) ? 0 : 1;
   }
   unsigned int bitVal = 0;
   unsigned int number = 0;
   if( (x & (1<<bitPos)) != 0)
   {
      if(r->left == NULL)
      {
         number = findMaxXOR(r->right, x, bitPos-1);
         bitVal = 0;
      }
      else
      {
         number = findMaxXOR(r->left, x, bitPos-1);
         bitVal = 1;
      }
   }
   else
   {
      if(r->right == NULL)
      {
         number = findMaxXOR(r->left, x, bitPos-1);
         bitVal = 0;
      }
      else
      {
         number = findMaxXOR(r->right, x, bitPos-1);
         bitVal = 1;
      }
   }
   if(bitVal == 0)
      number = number & ~(1<<bitPos); // Resetting bitPos
   else
      number = number | (1<<bitPos); // Setting bitPos
   return number;
}

Below is the final code, combining all above functions:

#include <iostream>
using namespace std;
struct Node
{
   Node *left, *right;
   // Constructor. Set left and right to NULL
   Node():left(NULL),right(NULL){}
};
// Create a trie from the values in the array
void insertValueInTrie(Node* r, unsigned int x)
{
   unsigned int N = sizeof(unsigned int) * 8;
   for(int i=N-1; i>=0; i--)
   {
      unsigned int bitValue = (x & (1<<i)); // Get i'th Bit of x
      if(bitValue != 0)
      {
         if(r->right == NULL)
            r->right = new Node();
         r = r->right;
      }
      else
      {
         if(r->left == NULL)
            r->left = new Node();
         r = r->left;
      }
   }
}
// Find Max XOR of x in the tree rooted at r.
unsigned int findMaxXOR(Node* r, unsigned int x, int bitPos)
{
   if(r == NULL || bitPos < 0)
      return 0;
   if(bitPos == 0)
   {
      if( (x & (1<<bitPos)) == 1)
         return (r->left == NULL) ? 0 : 1;
      else
         return (r->right == NULL) ? 0 : 1;
   }
   unsigned int bitVal = 0;
   unsigned int number = 0;
   if( (x & (1<<bitPos)) != 0)
   {
      if(r->left == NULL)
      {
         number = findMaxXOR(r->right, x, bitPos-1);
         bitVal = 0;
      }
      else
      {
         number = findMaxXOR(r->left, x, bitPos-1);
         bitVal = 1;
      }
   }
   else
   {
      if(r->right == NULL)
      {
         number = findMaxXOR(r->left, x, bitPos-1);
         bitVal = 0;
      }
      else
      {
         number = findMaxXOR(r->right, x, bitPos-1);
         bitVal = 1;
      }
   }
   if(bitVal == 0)
      number = number & ~(1<<bitPos); // Resetting bitPos
   else
      number = number | (1<<bitPos); // Setting bitPos
   return number;
}
void printMaxXORTrie(unsigned int * arr, int n)
{
   // ROOT NODE
   Node* r = new Node();
   int maxXOR = 0;
   for(int i=0; i<n; i++)
   {
      unsigned int t = findMaxXOR(r, arr[i], (sizeof(unsigned int)*8)-1 );
      if(t > maxXOR)
         maxXOR = t;
      insertValueInTrie(r, arr[i]);
   }
   cout<<"MAX XOR VALUES : "<<maxXOR<<endl;
}
int main()
{
   unsigned int arr[] = {12, 15, 5, 7, 1, 9, 8, 6, 10, 13};
   printMaxXORTrie(arr, 10);
}