Assign Mice to Holes
April 29, 2020Logger Rate Limiter Solution (LeetCode)
August 22, 2020Fitting Shelves Problem
Given the length of a wall w and infinite shelves of two lengths small and large (large > small).
Find the optimal solution to put the shelves in the wall such that the empty space left is minimum. We have to use the large shelves as much as possible (keeping the empty space minimum) because the large shelves are cheaper than the smaller ones.
Example: Input: WallLength = 24 smallShelfLength = 3 largeShelfLength = 5 Output: S: 3 L: 3 E: 0 Explanation: We use three units of both large and small shelves and 0 space is left empty. 3 * 3 + 3 * 5 = 24 Empty space = 0 Another solution could have been S: 8 L: 0 E: 0 but because the larger shelf is cheaper the previous solution should be the answer.
Solution:
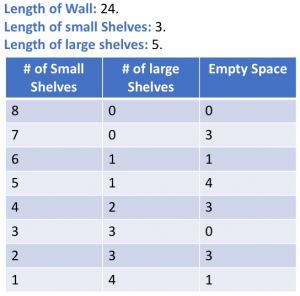
A simple solution is to try all possible combinations of small and large shelves.
- Start by putting the maximum number of small shelves (with zero large shelves)
- Keep reducing the number of small shelves and try to fit the maximum number of large shelves possible in the extra space.
The final answer is (3, 3, 0). 3 small Shelves, 3 large shelves and zero empty.
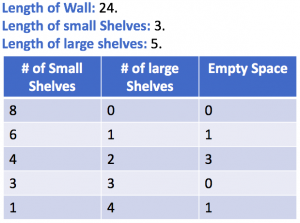
We can improve this brute-force way by increasing the number of large shelves in each iteration. So the number of rows in the above diagram will reduce:
The code for this is very simple as below:
Code:
void fittingShelves(int wall, int small, int large)
{
if(wall < small)
{
cout<<"Empty : "<<wall;
return;
}
// WHEN PUTTING ZERO LARGE SHELVES
int numSmall = wall / small;
int numLarge = 0;
// VALUES OF minEmpty ARRANGEMENT
int minEmpty = wall % small;
int minEmptySmall = numSmall;
int minEmptyLarge = numLarge;
while(true)
{
numLarge++;
if(numLarge * large > wall)
break;
int extra = wall - (numLarge * large);
// TRY TO PUT AS MANY SMALL AS POSSIBLE.
int numSmall = extra/small;
int empty = extra % small;
if(empty <= minEmpty)
{
minEmpty = empty;
minEmptySmall = numSmall;
minEmptyLarge = numLarge;
}
}
cout <<"\nS:"<<minEmptySmall <<" L:"<<minEmptyLarge <<" E:"<<minEmpty;
}
int main()
{
int wall = 24, m = 3, n = 5;
fittingShelves(wall, m, n);
wall = 24, m = 4, n = 7;
fittingShelves(wall, m, n);
wall = 7, m = 3, n = 5;
fittingShelves(wall, m, n);
wall = 29, m = 3, n = 9;
fittingShelves(wall, m, n);
cout<<"\n";
}
Output:
S:3 L:3 E:0 S:6 L:0 E:0 S:2 L:0 E:1 S:0 L:3 E:2