Dynamic Programming concept

The basic idea of DP is applicable to problems that can be thought in terms of recursion. For example, consider problem of computing n’th fibonacci term:

This is a recursive definition (Fib(n) is given in terms of Fib(n-1)) and can be adopted in the form of a function in a straight-forward way:

int fib(int n)
{
   if (n==1 || n==2)
      return 1;
   else
      return fib(n-1) + fib(n-2);
}

But, as we know that recursive codes are not optimised for memory or CPU time. It takes more memory (activation record is created per recursive call) and more CPU time.
One more problem with the above code is that it is solving a subproblem more than once. Consider the case when n=5, the function calls will be as shown below, value in the node represent the value of n.

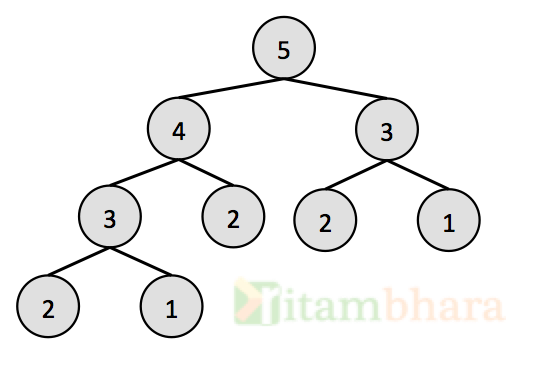
The function fib(n), where n=5, will call two function with n=4 and n-3. Function with n=4 will in turn call functions with n=3 and n=2. So the computation of fib(n) for n=3 is computed twice.

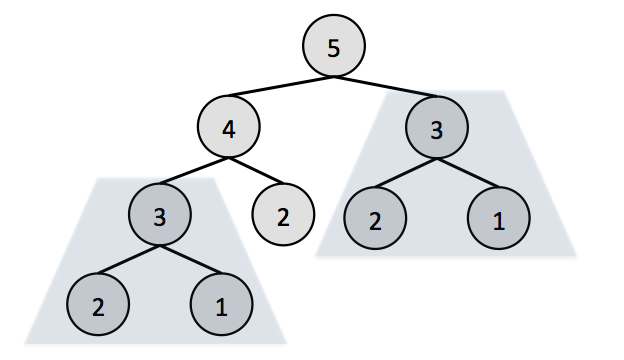
This function takes exponential time.
If we calculate the value of fib(20) using this method then fib(3) will be computed 2584 times and fib(10) will be computed 89 times. Had we been solving a sub problem only once, our code may become 1000 times faster. Dynamic programming is precisely for this purpose.

Memoized Dynamic Programming

When we store the solution of sub problems in some sort of dictionary and use the already solved result when the sub problem is encountered again (rather than solving the same subproblem again), it is called memorization.

In the above example, let us have an extra memory as integer array of size n, whenever k’th Fibonacci term is computed, store that number in k’th index of this array and when the recursive code calls the function again to compute k’th Fibonacci term then return this value (constant time operation) rather then computing it again (O(2^k) time operation).

//this array will store fib(k) at k'th index.
//memo[k]==0, indicate that fib(k) is not yet computed
int memo[N] = {0};
int fib(int n)
{
    //If fib(n) already computed, don't compute it again
    if(memo[n] != 0)
        return memo[n];
    // compute fib(n) and store it at n'th index in memo.
    if(n==1 || n==2)
        memo[n] = 1;
    else
        memo[n] = fib(n-1)+fib(n-2);
    return memo[n];
}

The time taken by this function will be O(n). Hence we have reduced the time taken from exponential to linear. Which is great. But, the code has two problems:

1. It is taking O(n) extra memory in the form of array to store the Fibonacci terms. To compute the n’th term we just need the (n-1)’th term and (n-2)’th term. So there seems to be a scope of reducing the extra memory being used.
2. We are still using lot of recursion. This is because we are solving the problem in a top-down manner, i.e we are starting with ‘n’ and not with the first term.

These problems can be solved using another form of Dynamic programming, the Bottom-up dynamic programming:

Bottom-up dynamic programming

We will start with first computing Fib(1), then Fib(2) and so on moving in the forward direction.

int fib(int n)
{
  // Array to store fib numbers
  int arr[N];
  arr[1] = 1;
  arr[2] = 1;
  for (int i = 2; i <= n; i++)
  {
      // compute fib(n) and store it
      arr[i] = arr[i-1] + arr[i-2];
  }
  return arr[n];
}

The recursion is unrolled and we move in a different direction than the memorized Dynamic programming. This function also takes linear time, but it is better than memorized DP, because there is no recursive function calls.

In fact, the above function can be further optimised on memory, because to compute the k’th fibonacci term, we just need (k-1)’th term and (k-2)’th term and not the previous terms, similarly, going forward, for (k+1)’th term we don’t even need (k-1)’th term. Hence the same memory locations can be reused.

int fib(int n)
{
    if(n==1 || n==2)
        return 1;
    int a = 1; // For (k-2)'th term term.
    int b = 1; // For (k-1)'th term
    int c;     // For k'th term
    for (int i = 3; i <= n; i++)
    {
        c = a + b;
        a = b;
        b = c;
    }
    return c;
}

Above function takes O(n) time and constant amount of extra memory and is hence optimised over both time and memory.

Dynamic programming problems are usually very complex problems, we have used a very basic example, to explain the concept.

Steps to solve any problem using Dynamic programming

1. See if DP is applicable. If a problem can be defined in terms of sub problems then chances are the DP can be used.
2. Defined Sub-Problems. Defined a bigger problems in terms of sub-problems, here we are defining in top-down manner, larger problem is defined in terms of smaller sub-problems.
3. Relate sub-problems. In this step see if a sub-problem is solved more than once (Overlapping subproblems.
4. Try memoization. If a subproblem is solved multiple times, then there is a scope to solve it only once, remember the solution and use that solution next time.
5. Try solving Bottom-up. This is the step where we try to eliminate the recursion and redefine the solution in forward direction.