Code to convert In-Fix to postfix notation

Given an arithmetic expression in in-fix notation. Write code to convert that algorithm in corresponding post-fix notation. For example:

   Infix          Postfix
   ------         --------
    a+b            ab+
    (a+b)*c        ab+c*
    a+b*c          abc*+
    a*(b+c)-d/e    abc+*de/-

Solution:

To solve this expression, we need a Stack. Let the Infix expression be in a String, and postfix expression will go in another string.
Initially the Stack will be empty and postfix expression will also be empty.
Algorithm:

1. Read the tokens(characters) from the infix string one at a time from left to right
2. If token is an operand, add it to the Postfix string.
3. If token is a Left parentheses, Push it on to the Stack
4. If the token is a Right parentheses
   1. Repeatedly Pop the stack and add the poped out token in to postfix string until a left parenthesis is encountered.
   2. Remove left parenthesis from the stack and ignore it
5. If token is an operator
   1. If the stack is empty push the operator in to the stack
   2. If the stack is not empty compare the precedence of the operator with the element on top of the stack
      1. If the operator in the stack has higher precedence than the token Pop the stack and add the poped out element in to the string S. else Push the operator in to the stack
      2. Repeat this step until the stack is not empty or the operator in the stack has higher precedence than the token
6. Repeat this step till all the characters are read.
7. After all the characters are read and the stack is not empty then Pop the stack and add the tokens to the string S
8. Return the Postfix string S

Lets follow an example visually:
Infix Expression: A * (B + C) – D / E

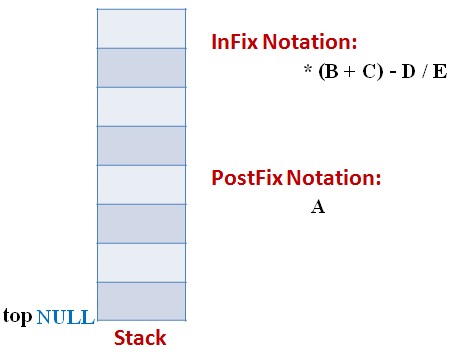
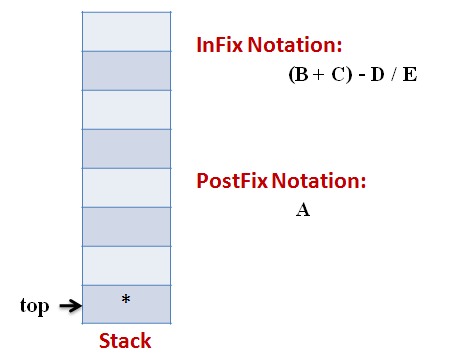
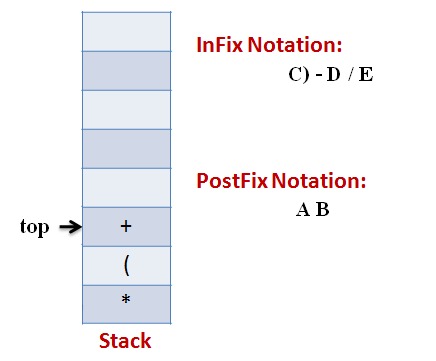
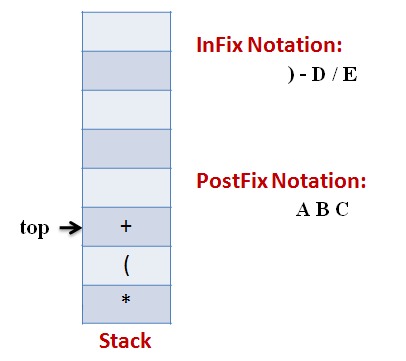
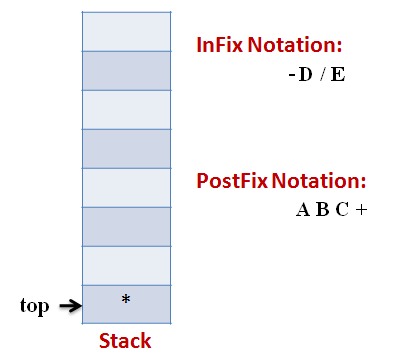
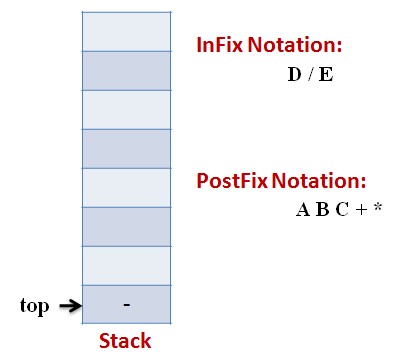
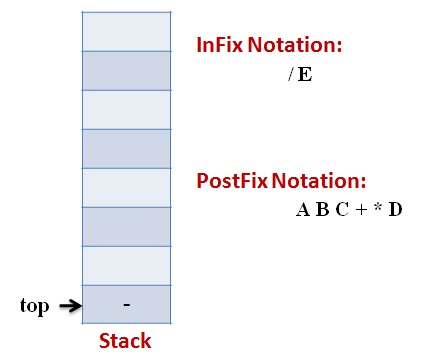
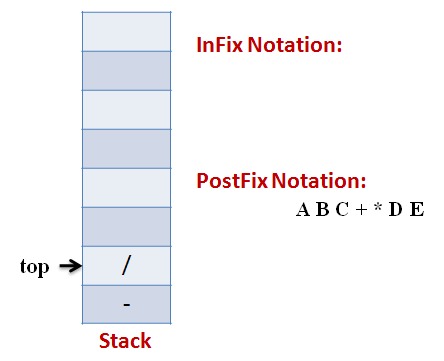
Code:

For simplicity of implementation, I assume that expression has only three things:

• Operators (^ representing power-of operator)
• Operands. All operands are single alphabets (either small case or capital case)
• parenthesis. The only type of braces allowed is parenthesis, ‘(‘ and ‘)’.

In this code we use the implementation of Stack from this post. Please read it before proceeding further.

Then we are using two helper function, one to check if the given character is operand or not and second to return the precedence of a given operator.

/*
 * operand can be a single alphabete only.
 */
bool isOperand(char ch)
{
   return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z');
}
/*
 * return the precedence of an operator. Numbers are just to use precedence for relative purpose.
 */
int operatorPrecedence(char ch)
{
   switch (ch)
   {
      case '+':
      case '-':
         return 1;
      case '*':
      case '/':
         return 2;
      case '^':
         return 3;
   }
   return -1;
}

Below is the function that does the actual operation. It just print the postfix expression and

/*
 * This function uses Stack data structure. Returns -1 if the expression is invalid
 */
int infixToPostfix(char* expression)
{
   int i, k;
   MyStack stack;
   // read each character of the expression (which is either operator, operand or parenthesis
   for (i = 0, k = -1; expression[i]; ++i)
   {
      if (isOperand(expression[i]))
      {
         expression[++k] = expression[i];
      }
      else if (expression[i] == '(')
      {
         stack.push(expression[i]);
      }
      else if (expression[i] == ')')
      {
         while (!stack.isEmpty() && stack.getTop() != '(')
            expression[++k] = stack.pop();
         if (!stack.isEmpty() && stack.getTop() != '(')
            return FAILOUR;
         else
            stack.pop();
      }
      else // an operator is encountered
      {
         while (!stack.isEmpty() && operatorPrecedence(expression[i]) <= operatorPrecedence(stack.getTop()))
            expression[++k] = stack.pop();
         stack.push(expression[i]);
      }
   }
   // All remaining elements in the stack are operators.
   // pop them all out
   while (!stack.isEmpty())
      expression[++k] = stack.pop();
   expression[++k] = '\0';
   cout<<expression ;
   return SUCCESS;
}