Array implementation of Queue data structure

To learn the basics of the Queue visit our previous post on implementing Queue using linked list. In case the Queue is implemented using Linked list Enqueue (insertion) is about inserting a new node at the end and Dequeue (removing an element) is about deleting the first node.
But, for array, things are little different.
Method-1: Not-So Efficient 

In this method we have two indexes (similar to two pointers in case of linked list implementation).

1. front – hold index of position from where element will be deleted.
2. rear – hold index of position where element will be inserted.

Initially, (when the Queue is empty), front will be -1 (because there is no element to be removed) and rear will be 0 (position where element will be inserted)

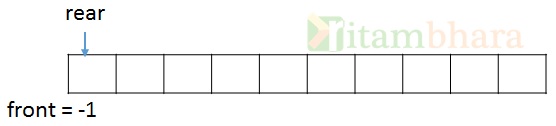
After inserting one element in the queue (say 2), the situation will look like:

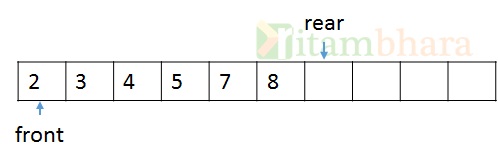
The rear pointer points to the next available (empty) position and front will point to the element which is to be deleted. Similarly, After inserting other elements, the rear pointer will move forward and always point to the next empty position

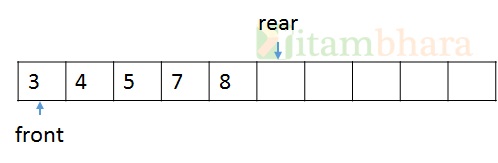
When an element is to be removed, the element will be removed from the front. But then all the elements will be shifted toward left, so that there is no hole in the queue.

Condition of the Queues will be

Queue Empty: any one of the two conditions can be used to check if the Queue is empty or not: (front == -1) OR (rear == 0)
Full Queue: (rear==n)

Code:

Actually we don’t need front pointer at all. because it always points to the first element and the condition of Empty queue can be checked with rear also. The class for Queue will look like below. The important thing to note is that size of queue will be fixed (unlike when we implement it using Linked List)

class QueueOnArray
{
public:
    // Constructor
    QueueOnArray(int n): rear(0), size(n){
        arr = new int[size];
    }
    // Destructor - delete the Queue
    ~QueueOnArray(){
        delete[] arr;
    }
    void enqueue(int data);
    int dequeue();
    bool isEmpty();
    void printQueue();
private:
    int rear;
    int size;
    int *arr; // Array to hold the queue
};

Code for Constructor and destructor is given in the above code itself, code for other functions is as below:

/**
 * Insert an element at the end of Queue.
 * If the Queue is full then throws an exception.
 */
void QueueOnArray::enqueue(int data)
{
    // case Queue is FULL
    if(rear == size){ throw; }
    arr[rear++] = data;
}
/**
 * Delete and return the first element of the queue.
 * If there are no element in the queue then the function will return -1.
 */
int QueueOnArray::dequeue()
{
    // If no element then return -1
    if(rear == 0){
        return -1;
    }
    int returnValue = arr[0];
    // Shift all the elements left by one position.
    for(int i=0; i<rear-1; i++)
    {
        arr[i] = arr[i+1];
    }
    rear--;
    return returnValue;
}
/**
 * return true if the Queue is empty, else return false.
 */
bool QueueOnArray::isEmpty()
{
    return (rear == 0);
}
/**
 * Print the entire Queue
 */
void QueueOnArray::printQueue()
{
    for(int i=0; i<rear; i++)
    {
        cout<<" "<<arr[i];
    }
}

The problem with this implementation is that the time complexity to delete element from Queue is O(n). Ideally inserting an element in queue and removing an element from queue should take constant time. So this is not the right kind of implementation.

Note: We can easily change the above code such that it will take, O(n) time in inserting and constant time to delete an element.

Method-2: Circular Queue

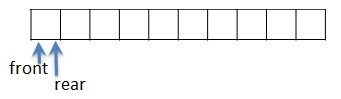
In this case there will be two pointers front and rear.

Initial state: Both front and rear are pointing to 0’th position

When an element is inserted in the Queue, then front pointer remains as it is, element is inserted at the rear position and rear is incremented using the formula

rear = (rear + 1) % SIZE

The state of Queue after inserting elements 2, 3, 4 and 6 will be as shown below.

Element  is deleted from the front position and then front is also incremented using the same logic:

front = (front + 1) % SIZE

After 2 is deleted the queue will look like:

This is just normal.. the difference will be seen when end point is reached. For example, after inserting few more elements and deleting some elements the queue will look like

When the queue is full then also front and rear will become equal. If we insert 3 more elements then the situation will be:

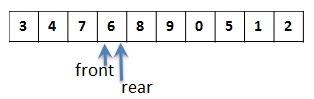
Hence, when (front == rear), we need to have some more way to distinguish between whether Queue is empty or full. So lets have one more flag which indicate whether its full or empty.

Hence, Initial state will be

front = 0;
rear = 0;
isEmpty = true;

Code:

class QueueOnArray
{
public:
    // Constructor
    QueueOnArray(int n): rear(0), front(0), size(n), empty(true){
        arr = new int[size];
    }
    // Destructor - delete the Queue
    ~QueueOnArray(){
        delete[] arr;
    }
    void enqueue(int data);
    int dequeue();
    bool isEmpty();
    void printQueue();
private:
    int rear;
    int front;
    int size;
    bool empty;
    int *arr; // Array to hold the queue
};

The initial condition is very clear in the constructor. Other functions will be as shown below (notice the difference in the printQueue function).

/**
 * Insert an element at the end of Queue.
 * If the Queue is full then throws an exception.
 */
void QueueOnArray::enqueue(int data)
{
    // case Queue is FULL
    if(rear == front && !empty){ return; }
    arr[rear] = data;
    rear = (rear + 1) % size;
    empty = false;
}
/**
 * Delete and return the first element of the queue.
 * If there are no element in the queue then the function will return -1.
 */
int QueueOnArray::dequeue()
{
    // If no element then return -1
    if(rear == front && empty){
        return -1;
    }
    int returnValue = arr[front];
    front = (front+1)%size;
    // If Queue has become empty. set the flag
    if(front == rear)
        empty = true;
    return returnValue;
}
/**
 * return true if the Queue is empty, else return false.
 */
bool QueueOnArray::isEmpty()
{
    return (rear == 0);
}
/**
 * Print the entire Queue
 */
void QueueOnArray::printQueue()
{
    cout<<"\n Queue is : ";
    if(empty)
        return;
    int i = front;
    do{
        cout<<" "<<arr[i];
        i = (i+1)%size;
    }while(i != rear);
    cout<<endl;
}

Time complexity: The above code will take constant time in both enqueue and dequeue operations.
Further Optimizing:

We can manage with 2 variables (rather than three variables front, rear and empty flag). If we just keep two variables

front – pointing at the first element of the queue.
count – holding the number of elements in the queue.

Initially count will be zero. When an element is inserted in the queue, count will be incremented and when an element is removed from the queue then it will be decremented.

Queue will be empty when (count==0)
Queue will be full when (count == size)

front will be incremented like front = (front +1) % size only.