Print all possible root-to-leaf paths in a binary tree

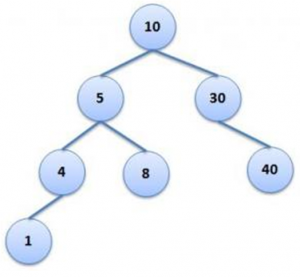Given a Binary Tree, write code to print all root-to-leaf paths possible in the tree. For Example, For the Binary Tree given on the right side, the output should be

10, 5, 4, 1
10, 5, 8
10, 30, 40

 Solution:

The problem in this one is how will you communicate the already computed path to the next level in the recursion. Let us use an array for this. The size of the array is O(h), where h is the height of the Binary Tree under question. For this question, I am taking a hard-coded array of size 100 (safe because we rarely find binary trees with that height).

Algorithm:

int arr[100] // hard-coded array to store intermediate paths
Function PrintPaths(Node* root)
    IF root is NULL
        return;
    IF root is LEAF NODE
        PRINT ARRAY arr
    ELSE
        APPEND root->data TO arr
        PrintPaths(root->LeftPointer)
        PrintPaths(root->RightPointer)

Code:

    /**
     * Function to print all the root-to-leaf paths in a binary tree.
     *
     * Parameters:
     *    root - Root of the Tree under consideration (in recursive calls root will be top of sub-tree)
     *    pathArr - Array to hold path data.
     *    pathCnt - index, where data need to be inserted in the pathArr
     */
    void printPaths(Node* root, int *pathArr, int pathCnt)
    {
        if (NULL == root)
            return;
        pathArr[pathCnt] = root->data;
        // If leaf then Print the Path
        if (root->lptr == NULL && root->rptr == NULL)
        {
            // Printing the Array
            printf("\n");    // to print paths in separate line
            for(int i=0; i<=pathCnt; i++)
                printf(" %d", pathArr[i]);
        }
        else
        {
            printPathsRecur(root->lptr, pathArr, pathCnt + 1);
            printPathsRecur(root->rptr, pathArr, pathCnt + 1);
        }
    }

You may call the above function like below:

    Node* root = NULL;
    // ...
    // Create the Binary Tree.
    // ...
    int path[100];
    printPaths(root, path, 0);

References:
http://cslibrary.stanford.edu/110/BinaryTrees.html